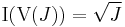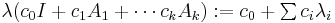Hilbert's Nullstellensatz
Hilbert's Nullstellensatz (German: "theorem of zeros," or more literally, "zero-locus-theorem" – see Satz) is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields. This relationship was discovered by David Hilbert who proved Nullstellensatz and several other important related theorems named after him (like Hilbert's basis theorem).
Contents[hide] |
Formulation
Let k be a field (such as the rational numbers) and K be an algebraically closed field extension (such as the complex numbers), consider the polynomial ring k[X1,X2,..., Xn] and let I be an ideal in this ring. The affine variety V(I) defined by this ideal consists of all n-tuples x = (x1,...,xn) in Kn such that f(x) = 0 for all f in I. Hilbert's Nullstellensatz states that if p is some polynomial in k[X1,X2,..., Xn] which vanishes on the variety V(I), i.e. p(x) = 0 for all x in V(I), then there exists a natural number r such that pr is in I.
An immediate corollary is the "weak Nullstellensatz": The ideal I in k[X1,X2,..., Xn] contains 1 if and only if the polynomials in I do not have any common zeros in Kn.
When k=K the "weak Nullstellensatz" may also be stated as follows: if I is a proper ideal in K[X1,X2,..., Xn], then V(I) cannot be empty, i.e. there exists a common zero for all the polynomials in the ideal. This is the reason for the name of the theorem, which can be proved easily from the 'weak' form using the Rabinowitsch trick. The assumption that K be algebraically closed is essential here; the elements of the proper ideal (X2 + 1) in R[X] do not have a common zero. With the notation common in algebraic geometry, the Nullstellensatz can also be formulated as
for every ideal J. Here, 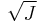 denotes the radical of J and I(U) is the ideal of all polynomials which vanish on the set U.
denotes the radical of J and I(U) is the ideal of all polynomials which vanish on the set U.
In this way, we obtain an order-reversing bijective correspondence between the affine varieties in Kn and the radical ideals of K[X1,X2,..., Xn]. In fact, more generally, one has a Galois connection between subsets of the space and subsets of the algebra, where "Zariski closure" and "radical of the ideal generated" are the closure operators.
Generalization
This generalization is due to Bourbaki, and is the most general form of the Nullstellensatz.
Let  be a Jacobson ring. If
be a Jacobson ring. If  is a finitely generated R-algebra, then
is a finitely generated R-algebra, then  is a Jacobson ring. Further, if
is a Jacobson ring. Further, if 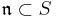 is a maximal ideal, then
is a maximal ideal, then 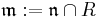 is a maximal ideal of R, and
is a maximal ideal of R, and 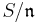 is a finite extension field of
is a finite extension field of 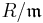 .
.
Another generalization states that a faithfully flat morphism 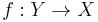 locally of finite type with X quasi-compact has a quasi-section, i.e. there exists
locally of finite type with X quasi-compact has a quasi-section, i.e. there exists 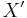 affine and faithfully flat and quasi-finite over X together with an X-morphism
affine and faithfully flat and quasi-finite over X together with an X-morphism 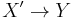 .
.
Applications
Commuting matrices
The fact that commuting matrices have a common eigenvector – and hence by induction stabilize a common flag and are simultaneously triangularizable – can be interpreted as a result of the weak Nullstellensatz, as follows: commuting matrices form a commutative algebra
![K[A_1,\ldots,A_k]](/2012-wikipedia_en_all_nopic_01_2012/I/dbda72e2b1b61f51a1442bd1781ff5de.png) over
over ![K[x_1,\ldots,x_k];](/2012-wikipedia_en_all_nopic_01_2012/I/98be5069f883ae1bee0f0e095c142193.png)
the matrices satisfy various polynomials such as their minimal polynomials, which form a proper ideal (because they are not all zero, in which case the result is trivial); one might call this the characteristic ideal, by analogy with the characteristic polynomial.
One then defines an eigenvector for a commutative algebra as a vector v such that for all 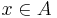 one has
one has 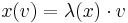 for a linear functional
for a linear functional
This simply linearizes the definition of an eigenvalue, and is the correct definition for a common eigenvector, as if v is a common eigenvector, meaning 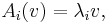 then the functional is defined as
then the functional is defined as
(treating scalars as multiples of the identity matrix 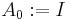 , which has eigenvalue 1 for all vectors), and conversely an eigenvector for such a functional
, which has eigenvalue 1 for all vectors), and conversely an eigenvector for such a functional  is a common eigenvector. Geometrically, the eigenvalue corresponds to the point in affine k-space with coordinates
is a common eigenvector. Geometrically, the eigenvalue corresponds to the point in affine k-space with coordinates  with respect to the basis given by
with respect to the basis given by 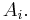
Then the existence of an eigenvalue  is equivalent to the ideal generated by (the relations satisfied by)
is equivalent to the ideal generated by (the relations satisfied by) 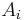 being non-empty, which exactly generalizes the usual proof of existence of an eigenvalue existing for a single matrix over an algebraically closed field by showing that the characteristic polynomial has a zero.
being non-empty, which exactly generalizes the usual proof of existence of an eigenvalue existing for a single matrix over an algebraically closed field by showing that the characteristic polynomial has a zero.
See also
References
- Shigeru Mukai; William Oxbury (translator) (2003). An Introduction to Invariants and Moduli. Cambridge studies in advanced mathematics. 81. p. 82. ISBN 0-521-80906-1.
- David Eisenbud, Commutative Algebra With a View Toward Algebraic Geometry, New York : Springer-Verlag, 1999.